The challenges of high dimensionality in short text clustering and using GSDMM to combat sparsity. (This is part 1 of 2 in a series showing the theory and application of GSDMM)
High in Fibre(er)?! Of Course.
Note: I generally add a few personal anecdotes to my writing, but if that doesn’t appeal to you the meat and potatoes begin in the second section “What is GSDMM?”
The Problem
Recently I’ve been reading Ayn Rand’s Atlas Shrugged (I know…harken back to the days of high school English Literature when I should have originally read it but did not). Ayn Rand is a lot of things, but brief is certainly not one of them. In no less than 1000 pages, Rand constructs scenes and characters in a masterpiece of careful consideration. As if I must know the color underneath the leaves outside the window as Reardon enjoys a sip of slightly watered whiskey. I’ve spent so much time reading article snippets, news summaries, and listening to elegantly summarized podcasts that I’ve forgotten just how to truly become engulfed in an author’s brain. I have become so acutely aware of Ayn Rand’s writing style over the past 1000 pages that I may even be able to reproduce it. This got me to thinking of how my brain has constructed a pretty excellent natural language processor for this author given the large amount of data I have provided it with. But I read articles, texts, tweets, etc. all the time and, although the understanding is different, I am still able to draw some conclusions given the assimilation of material over time. How does my comprehension of material in short text differ from the long-winded monologues of Ayn Rand? Is there a difference in the way my brain approaches the problem of many short snippets vs one long passage?
Given that many machine learning models are built on an assumption of how our brains process information, I think it’s useful to consider these questions as we approach new problems. And short text clustering is a traditionally difficult problem for a few reasons:
TF-IDF has less significance due to the low volume of words in a sentence compared to a passage. If all word frequencies in a sentence are 1 (because the sentence is short with no repeating words) then what value have I gained?
Using vector space for high dimensional data results in sparsity. This causes high compute and memory storage.
The result of problems 1 and 2 is that determining the number of clusters to separate the text is increasingly challenging and thus we lose the ability to interpret our data into topics.
What is GSDMM?
GSDMM (Gibbs Sampling Dirichlet Multinomial Mixture) is a short text clustering model proposed by Jianhua Yin and Jianyong Wang in a paper a few years ago. The model claims to solve the sparsity problem of short text clustering while also displaying word topics like LDA. GSDMM is essentially a modified LDA (Latent Dirichlet Allocation) which assumes that a document (tweet or text for instance) encompasses 1 topic. This differs from LDA which assumes that a document can have multiple topics. As I stated earlier in the pitfalls of TF-IDF, weighing multiple topics in a document is not a good approach for short text documents due to sparsity.
The basic principle of GSDMM is described using an analogy called “Movie Group Approach”. Imagine a group of students (documents) who all have a list of favorite movies (words). The students are randomly assigned to K tables. At the instruction of a professor the students must shuffle tables with 2 goals in mind: 1) Find a table with more students 2) Pick a table where your film interests align with those at the table. Rinse and repeat until you reach a plateau where the number of clusters does not change.
A good intuitive description of the differences between LDA and GSDMM can be found here while a more in-depth analysis of LDA can be found here. I’ll focus in this post on the parameters and derivation of the GSDMM model described in the paper by Yin and Wang.
Dirichlet Multinomial Mixture
For the first part of this model, it is important to understand what a Dirichlet distribution is. The Dirichlet distribution is essentially a Beta distribution over many dimensions (documents). And a Beta distribution is simply a distribution of probabilities that represent the prior state likelihood of a document joining a cluster as well as the similarity of that document to the cluster. Two parameters (alpha and beta described below) control the shape of the Beta distribution.
Components of DMM
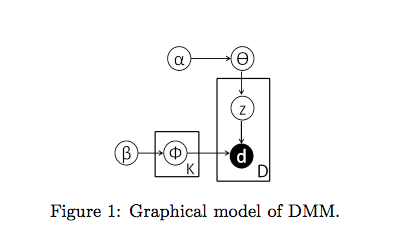From Yin and Wang paper
Let’s go through the key parameters comprising this model:
alpha: As described above alpha is a parameter affecting the shape of our probability distribution. More importantly, alpha is derived from the probability that a document will be grouped into a cluster. In the movie example, this is the probability of a student choosing a table.
beta: Beta is the other shape parameter for our distribution. Beta comes from the similarity of words in a document to those of words in another document. Relating to the movie groups, beta is the probability that a student will join a table with similar movie choices. If beta is 0, for example, the student will only join tables with movies in common. This may not be the best strategy. Perhaps 2 students have lists of thriller movies, but they’re not the same movies. We still want the students to wind up in the same group of thriller movies.
phi: Using k number of clusters (mixtures), phi is the multinomial distribution of clusters over words such that p(w|z = k) = phi where w = words and z = cluster label
theta: Similarly, theta is a multinomial distribution taking into account alpha, so p(d|z=k) = theta where d = document.
These parameters culminate in the probability that a document (d) is generated by a cluster (k) assuming Dirichlet priors.
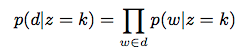From Yin and Wang paper
Additionally, it’s important to point out that the paper assumes symmetric Dirichlet priors. This means the same alphas and betas are assumed at the start. Alpha indicates the same clusters are equally important while beta indicates the same words are equally important. Yin and Wang indicate that in future iterations of this algorithm betas should not have symmetric priors, and instead more popular words should have less importance. If a word shows up in every document it isn’t a very valuable signal (see pitfalls of TF-IDF again).
Gibbs Sampling
Gibbs sampling describes the method of iterating through and reassigning clusters based on a conditional distribution. In the same way that the Naive Bayes Classifier works, documents are assigned to clusters based on the highest conditional probability.
Other Short Text Algorithms
I’ve focused on GSDMM because I learned the most about it through a personal project (see next post). There are other methods for short text clustering, but I have noticed that DMM is an underlying principle to many of these (GPU-DMM and GPU-PDMM adding in word embeddings), so I believe understanding these parameters and basic building blocks will serve well to developing more complex models.
References
The original paper by Yin and Wang here
This article summarizes GSDMM pretty well with relation to LDA and application.
I didn’t dive too deep into Gibbs Sampling. Another good article for LDA and Gibbs is here